How to enjoy teaching long division method in year 6

Believe it or not, the long division method in year 6 is actually one of my favourite maths topics to teach. At first glance, it can seem complex, off-putting, and unnecessary - but once pupils understand the step-by-step process, they start to see how clear and logical it really is.

We know that the SATs arithmetic paper is typically where pupils can achieve the highest scores in the maths test,  yet valuable marks are often lost due to small calculation errors. In an arithmetic paper, there are two questions involving division by a two-digit number (a 3-digit by 2-digit and a 4-digit by 2-digit), each worth two marks – that’s a full 10% of the paper’s marks. This is why it’s so important that children are confident and precise when it comes to division.

What is long division?

Year 6 pupils should learn to “divide numbers up to 4 digits by a two-digit whole number using the formal written method of long division, and interpret remainders as whole number remainders, fractions, or by rounding, as appropriate for the context” according to the National Curriculum.

Note that this doesn’t mean children must use the long division method when dividing by two-digits - they can use short division if they’d prefer - but as I’ll explain later on, for most children, long division is generally more accurate.

Mathematics Appendix 1 provides examples of formal written methods for all four operations, including long division, to show the range of approaches that might be taught. (It also notes that “for division, some pupils may include a subtraction symbol when subtracting multiples of the divisor” - just in case you were wondering about that extra minus sign!)

The first two methods shown are often referred to as the ‘chunking’ method, while the third example is the more traditional long division approach, and the one we’ll be focusing on here. It also happens to be my personal favourite!

Related content:

Ideas for year 6 maths after SATs

KS2 SATs 2025: maths papers analysis

10 common SATs maths mistakes and how to fix them

The importance of mental maths skills for SATs success

Short division vs. long division

Let’s be honest - the name ‘long division’ doesn’t do much to convince you otherwise. But once you’re confident with the method, it can actually be just as quick – if not quicker – than short division.

Is long division unnecessarily time-consuming?

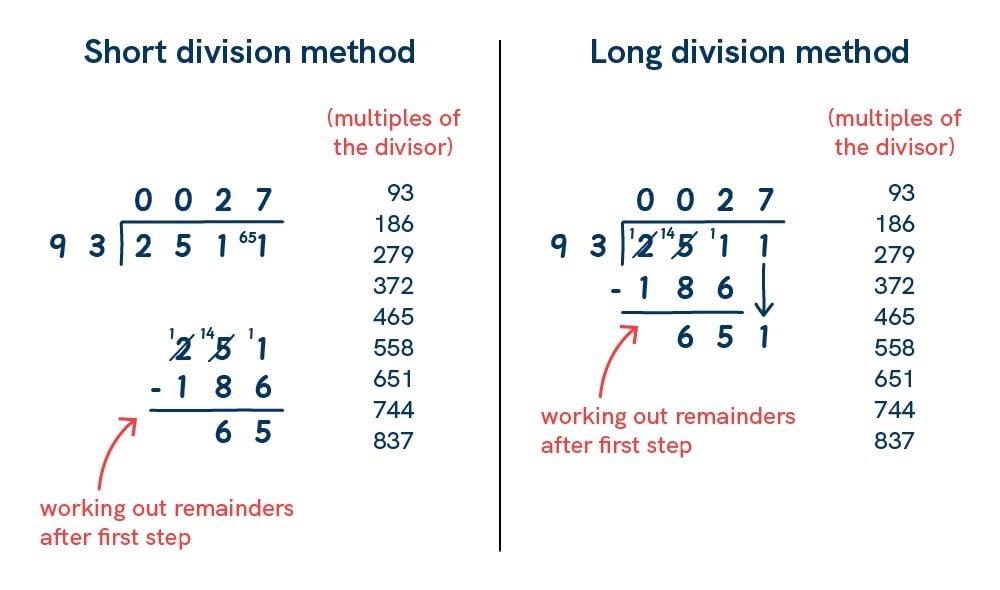
Take a look at the examples below, where 2,511 is divided by 93 using both short and long division.

With the short division method, children still have to work out remainders – and more often than not, that means written subtraction anyway. Even those who try to do it mentally (usually the ones who insist they don’t need to show their working!) are more likely to make mistakes when rushing.

In fact, using the long division method ended up being faster in this case, simply because I didn’t have to keep rewriting numbers all over the place when working out remainders – everything’s built into the structure.

Is long division unnecessarily complex? 

I’ll be honest: when I first started teaching year 6, I avoided long division for quite a while. I never really got it myself, despite feeling fairly confident in maths overall, so I couldn’t quite see the point of it. But when I finally sat down and took the time to properly learn the method, everything clicked. I realised just how structured and logical it actually is, and how clearly it shows what’s going on at each step of the division process. It’s a brilliant tool - especially for children who find maths tricky and need that clarity.

A little anecdote: during SATs last year, one of my ‘on the cusp’ pupils (you know the type, knew what they were doing but had very low confidence and were often overwhelmed by maths) was working through the arithmetic paper. I happened to glance over just as they tackled a long division question. Slowly, carefully, they made their way through each step, and got the answer spot on. This was the same child who didn’t even know their times tables at the start of the year. I honestly could’ve burst with pride.

Long division steps

Let me walk you through this tried and tested method of how to approach long division with year 6. Usually it would take me around three days in total, but as we all know, this is cohort-dependent. I’ve broken the process down into ‘steps’ instead so it can be spread across as many lessons as needed. 

Step 1 

Recap short division, ensuring children can talk through the process. Do they understand what’s happening at each step? For example, you could ask: 

• What is the divisor? 

• Why is it important to know multiples of the divisor? 

• What is a remainder? 

• How have you calculated the remainder? 

• What happens if you get a remainder at the end of the question? 

• How can you check if your calculation is correct? 

Once children are confident with short division, they can move onto long division. 

Step 2 

Dividing by 3? No big deal. Dividing by 97, like in the 2018 SATs paper? Suddenly a lot more daunting!

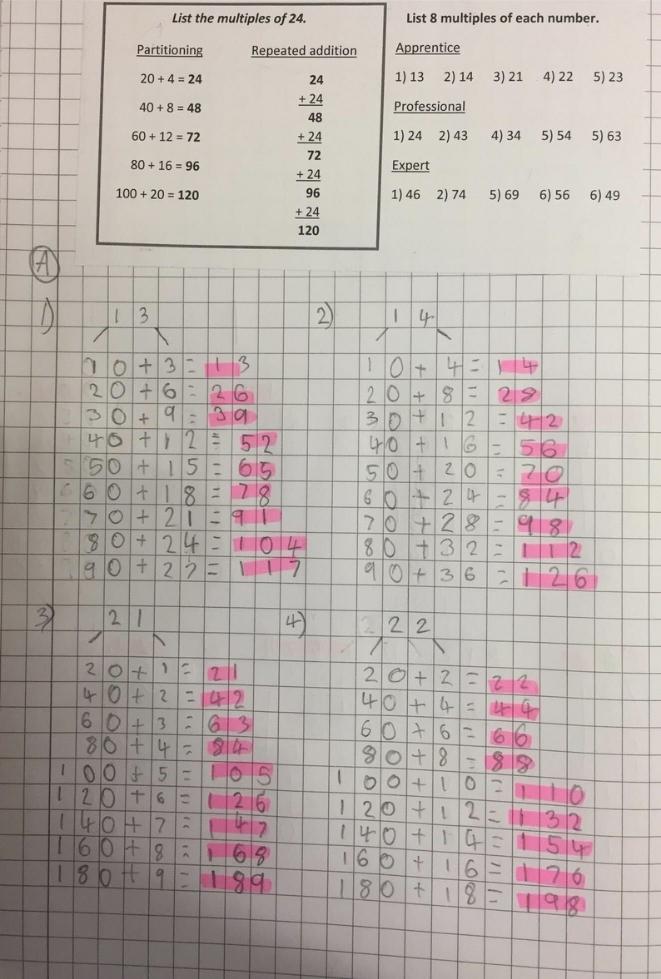
I always kick off this lesson by asking the class to list the first nine multiples of a ‘tricky’ number – something like 86. Cue the groans, frantic column addition, finger-counting, and all sorts of wonderfully inefficient strategies. (Every now and then, there’s a child who flies through it – we all know those who could rattle off multiples of 97 by adding 100 and subtracting 3 each time. Impressive, but unless your entire class is made up of children like this, this method still earns its place.)

That’s when I introduce partitioning. It’s one of those brilliant moments where you can almost see the cartoon lightbulbs switching on above their heads. And yes, it usually comes with a satisfying chorus of “Ohhhhhh yeahhhhhh!”

Step 3 

The good old ‘me, we, you’ process. Firstly, I show them a completed modelled example.  

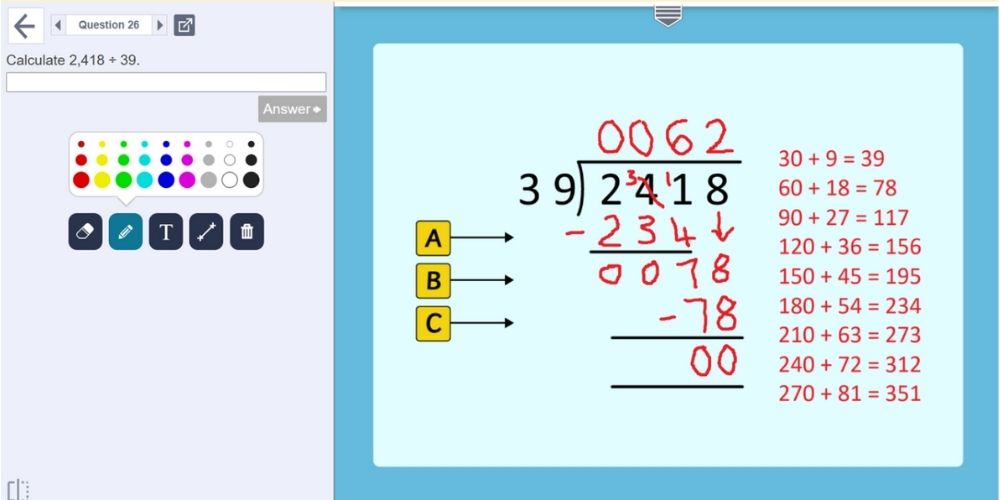
Then, I complete the division myself (next to the modelled example) to show them how I achieved it, always talking through each step as I go. This is usually when you get the “What?”, “Miss, I don’t get it”, or, “That’s impossible” comments - but it doesn’t take much to change their minds! 

It’s important to explain the steps broken down: to divide, multiply, subtract, then bring the next number down. I encourage the children to write the four symbols down on their page to remind themselves of the steps. They should have a solid understanding of these steps as, apart from the last one, they are the same as the short division process: 

• Divide: how many times does the divisor fit into the number without remainder? (use the list of multiples) 

• Multiply: multiply the answer to your previous division by the divisor to reach the multiple needed to calculate the remainder (use the list of multiples) 

• Subtract: subtract the multiple from the original number to calculate the remainder  

• Bring the next digit down: this replaces the ‘write the remainder just before the next number’ step in short division 

(Numbers 2-5 come from this Long Division rap video, purely because after watching this, it’s impossible to forget the order of the steps!) 

This method is far more coherently explained in the context of a specific question. Sometimes it’s appropriate to apply it to a division by a 1-digit number, to show how ‘long division’ is just a different way of setting out what they know as ‘short division’, but otherwise you can go straight into dividing by 2-digit number. We’ll walk through each stage in the next section.

Step 4 

Repetition, repetition, repetition. Do plenty together on whiteboards, gradually reduce the support, and then let the children go solo when they’re ready. In my classroom, this ends up looking like a kind of ‘peeling away’ process.

It usually goes something like this: 

1. I start with a 5-minute whole-class input.

2. After this, a few children feel confident enough to get going independently straight away.

3. I continue with the rest of the class for another 5 minutes.

4. After this, another group heads off to work on their own.

5. After another 5 minutes, a third group is ready to go.

6. By that point, I’m now left with the children who need the most support - either I work with them directly while my TA supports the rest of the class, or I switch roles with my TA depending on the need.

This way is both flexible and responsive - and it works well! 

Step 5 

Once the children are comfortable with the method, you can introduce reasoning activities, like long division with missing digits or “spot the mistake” challenges.

How to do long division by a 2-digit number

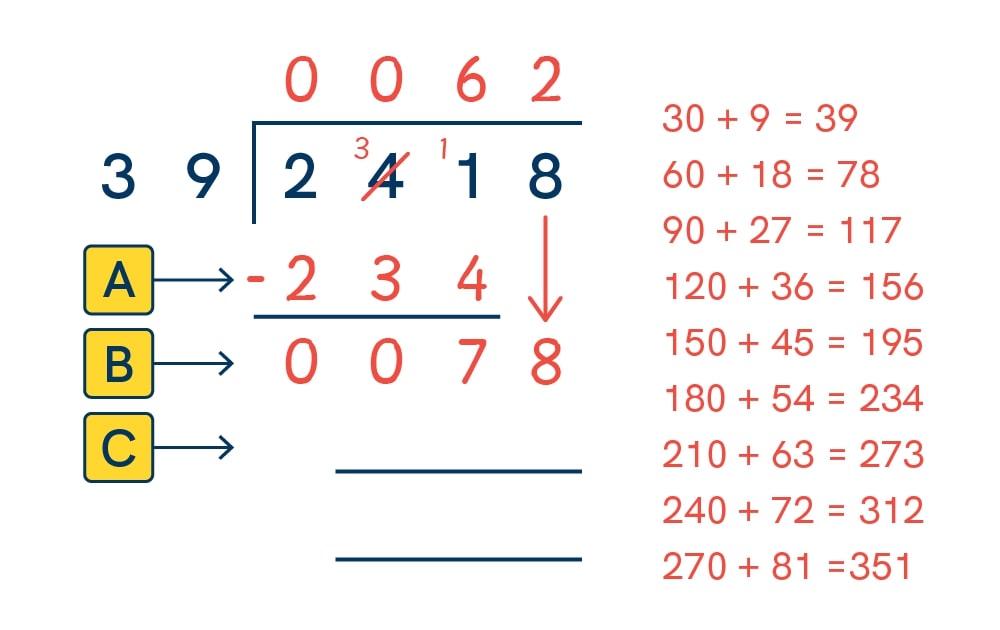
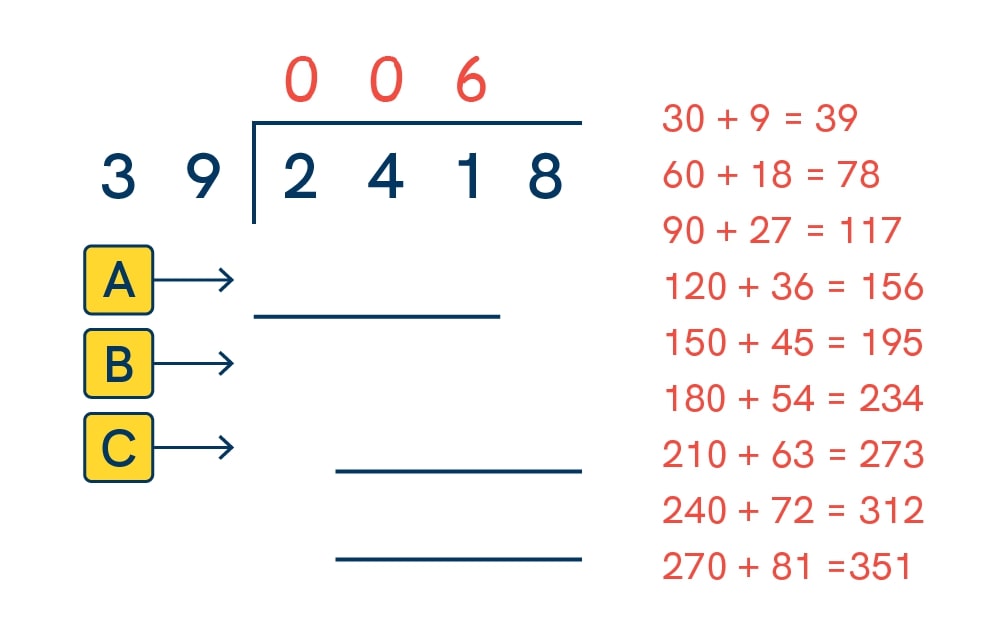
Let’s take the modelled example from Step 3 above, 2,418 ÷ 39:

1. Divide: 

241 tens ÷ 39 = 6 tens (I can see by looking through my list of multiples that 241 would be placed between 234, the 6^th multiple, and 273, the 7^th multiple). Note: as we’re working digit by digit from left to right, we can see that 39 doesn’t fit into 2 (the 1^st digit), therefore a 0 is placed above it; it also doesn’t fit into 24 (the 1^st and 2^nd digit combined), therefore another 0 is placed above it. We are now working with 241 (the first three digits combined) which has ensured that all the place values are correctly aligned)

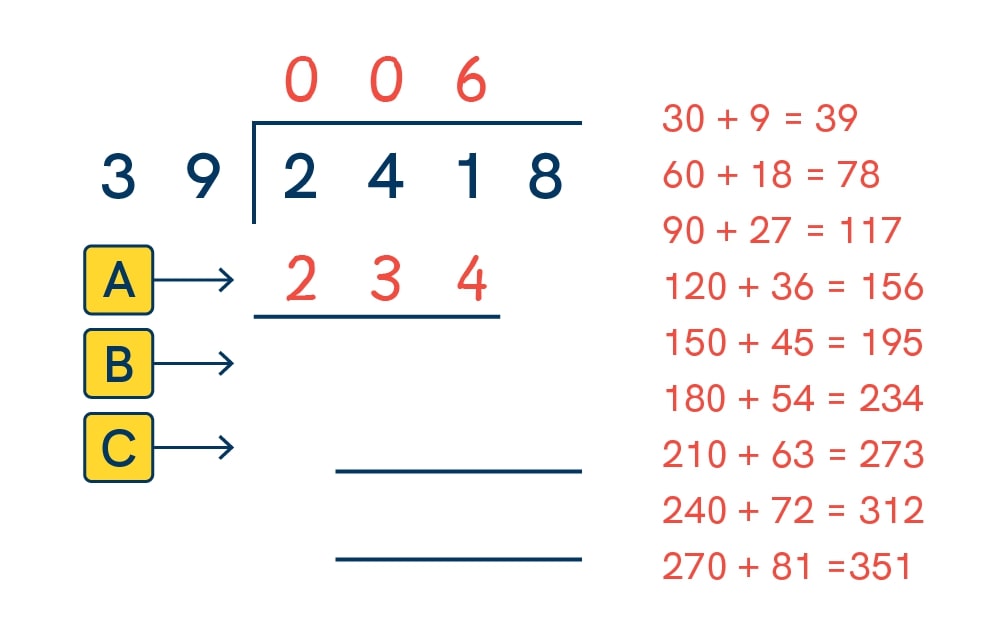
2. Multiply: 

6 lots of 39 is 234 (I should know this from the answer to the previous step, but I can also count down my list of multiples to find the 6^th multiple of 39). This is the number we need to work out the remainder to our first division (241 ÷ 39). 

3. Subtract: 

241 – 234 = 7, so this is the remainder to the first division (241 ÷ 39). This needs to be included in our next step.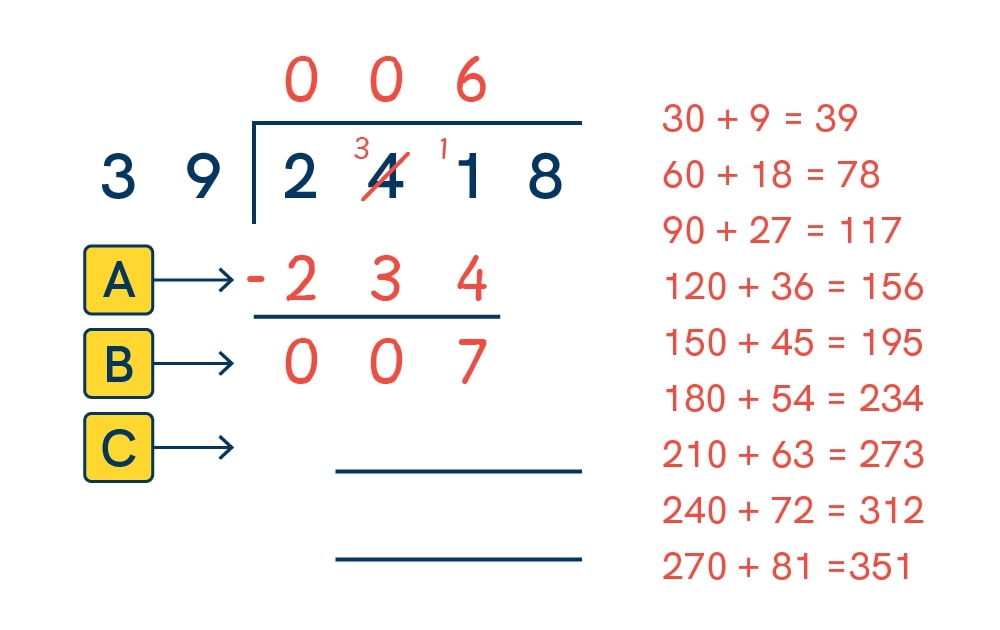

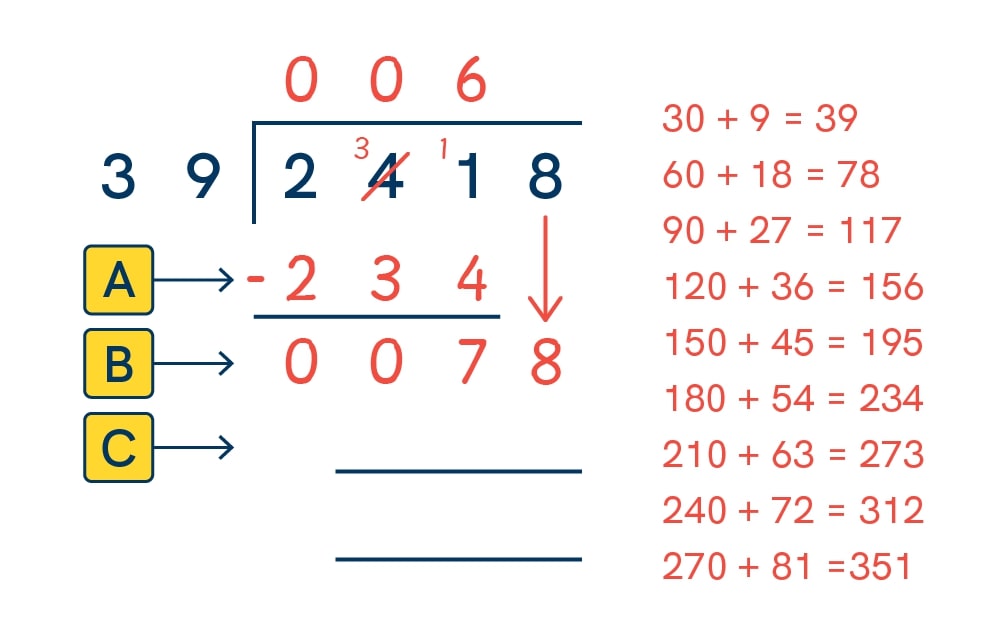
4. Bring the next digit down: 

Bringing the 8 down makes my new number 78. I’ll the repeat the process again.

5. Divide again:

78 ÷ 39 = 2, which is placed above the 8 (I can see this easily by looking through my list of multiples)

6. Multiply again: 

2 lots of 39 is 78 (I should know this from the answer to the previous step, but I can also count down my list of multiples to find the 2nd multiple of 39). 

7. Subtract again:

78 – 78 = 0. There is no remainder, so we know that the divisor must fit into the original number exactly. 

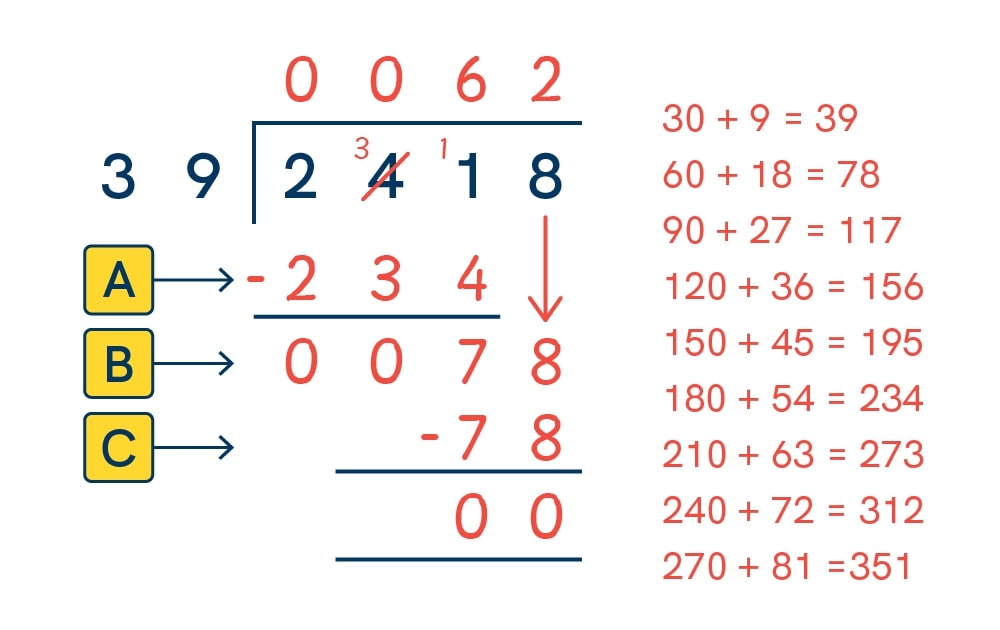
8. Check your answer:

Of course, like in any activity the children do, it’s important to encourage them to check their own work. They can do this by multiplying their answer by the divisor to see if the original number is produced. In this case, 62 x 39 = 2,418, so we know that we are correct. If they don’t get the original number as their answer, I’ve found that the most common mistake the children make is either listing the multiples incorrectly or misaligning the place values (meaning they may have calculated one of the steps with the wrong numbers).

Long division with remainders

If, when you reach the end of the method, you don’t get an answer of 0 (see part 7 above: ‘subtract again’), then your division has a remainder.

In the example below, when dividing 6,425 by 54, we are left with 53 as a remainder. This can be expressed in three ways: as a simple remainder (r 53), a fraction (53/54), or a decimal (.98 to two decimal places).

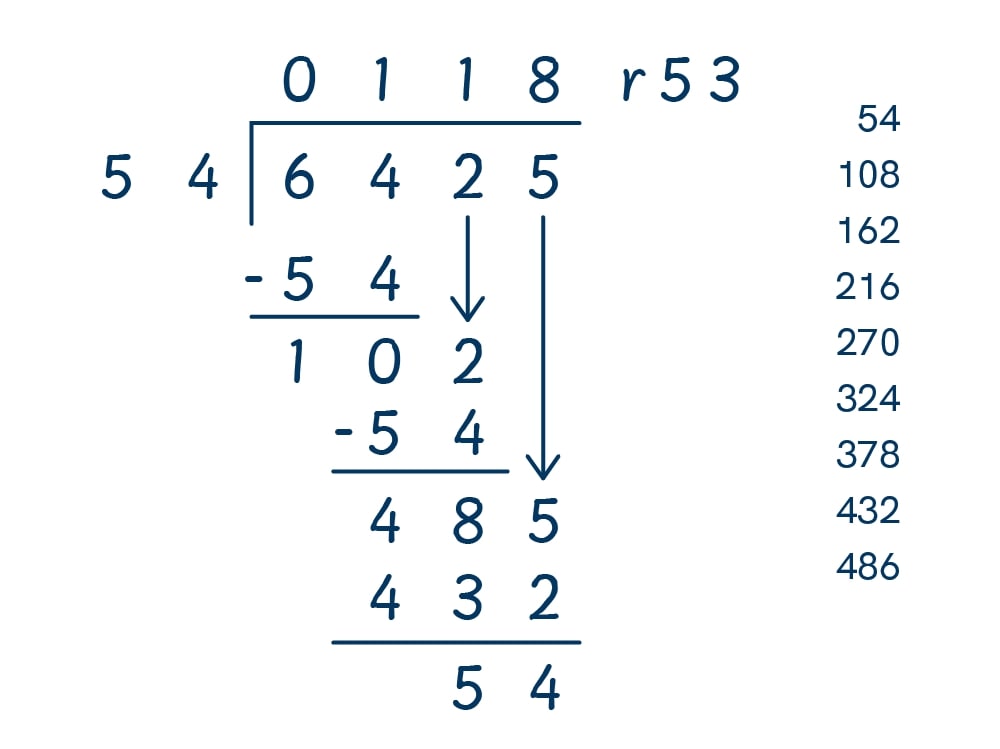
Expressing remainders as fractions

To express a remainder as a fraction, simply turn it into the numerator of a fraction, with the denominator being the divisor (in the example above, there are 53 54ths left over).

Expressing remainders as decimals

To express a remainder as a decimal is a little trickier. This isn’t often a requirement in year 6 (and if it is, the remainder wouldn’t be more than two decimal places long), but it can still be helpful to know. If the decimal places did continue past two, it is commonplace to round them to the nearest two decimal places. To calculate this, place zeroes as decimal places after the dividend (the number being divided) and divide as normal.

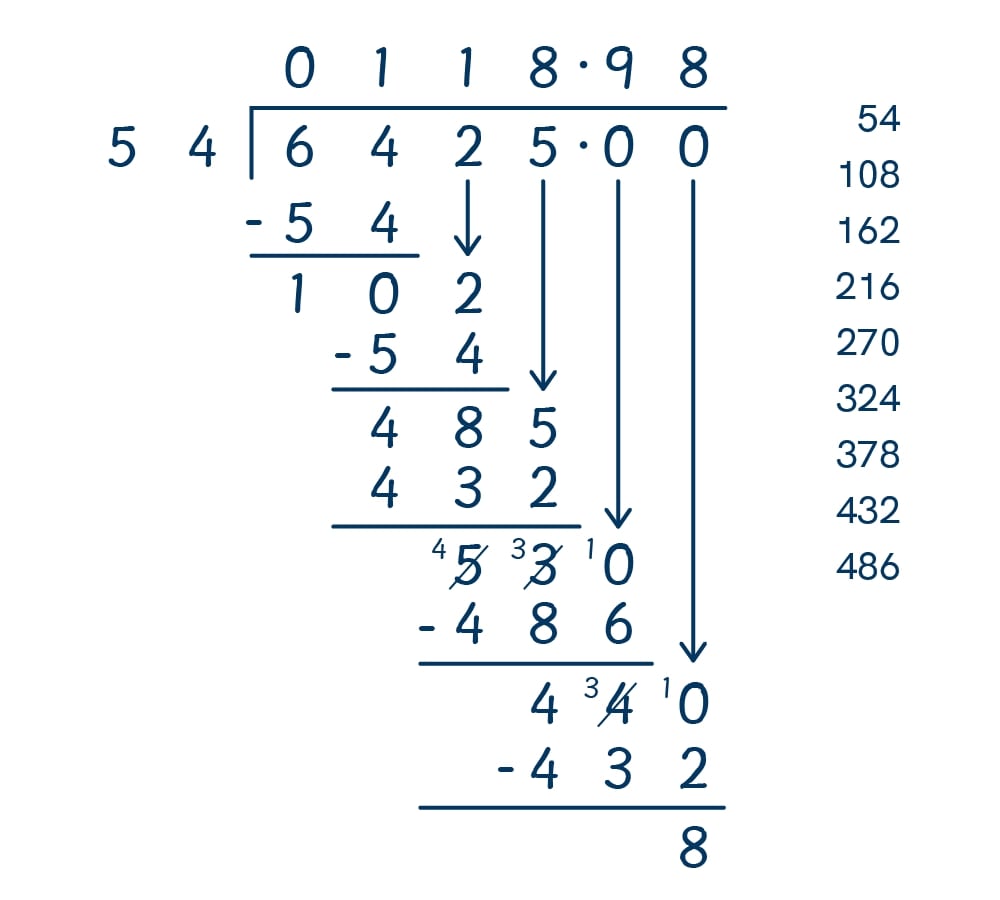
Whilst there has never been a long division question with a remainder in the arithmetic paper (the first, and only, short division question with a remainder appeared in 2023), there have been occasions in the reasoning paper where children were required to interpret a remainder when dividing by a 2-digit number - likely by using long division.

For example, in 2024, for two marks, children were asked the following question:

Mrs Mills has 940 seeds to plant into trays. She plants 12 seeds in each tray. The last tray is not full. What fraction of the last tray is filled?

This question could be answered using the long division method, but as most children should be confident in their 12 times tables, it could just as easily be solved using short division.

Long division may seem daunting at first, but once students grasp its logical structure, it becomes a clear and useful tool. By breaking it down step-by-step and practising regularly, they can build both confidence and accuracy. Of course, if you’re not confident with the method yourself, teaching it effectively will be a challenge. As with anything in teaching, it’s about finding what works for you and your class. But, given the ongoing debates on platforms like X and Facebook, I’m hopeful I’ve won a few converts to the long-division fan club!

If you’d like some extra support with your year 6s and the SATs, you can trial SATs Springboard from LbQ for free with no obligation to purchase.